How Tire Pressure Varies with Temperature

Based on discussions with the folks at SmarTire, with help from the members of CFG's 996 Forum.

For the range of temperatures and pressures we care about, the Ideal Gas Law

PV = nRT

is a good approximation of the behavior of the air in the tire. In this equation:

P	is the absolute (not gauge) pressure.
V	is the internal volume of the tire and rim combination.
n	is the amount of air in the tire. We won't worry about the units here; you can think of n as being the mass of the air, if you like.
R	is a constant. The value depends on the units we use; again, we won't worry about it here.
T	is the absolute (i.e. above absolute zero) temperature.

It's hard to make much use of this because there are so many variables. For example, there's no easy way for most of us to measure the mass of air in our tires, or the volume of the tire/rim combination.

Fortunately, we can simplify things. For a given radial tire on a given rim, the volume is essentially constant over a wide range of temperatures and pressures. (This is not true of bias-ply tires, and it's one of the reasons why it's hard to tell from a quick look whether a radial tire is underinflated.) Once you've inflated the tire, the amount of air in it is also essentially constant. So most of the time, the only things that vary are the pressure and temperature, and that variation is nice and linear:

P = (nR/V) T

The first step in making use of this is to measure gauge pressure (let's call it P') and relative temperature (let's call it T'.) If you have a SmarTire system or equivalent, you can read these two values directly. Otherwise, you'll need to wait for your tire to reach equilibrium with the outside air and use the outside temperature as an approximation for T'. You can measure P' with a regular tire gauge.

The next step is to convert from relative to absolute units. I'll use the old Imperial units here because most people reading this are in the US, but conversion is straightforward.

To change PSI gauge to PSI absolute, just add the atmospheric pressure at your location. The standard value at sea level is 14.7 PSI.

P = P' + 14.7

To convert to absolute temperature, add 459.7 (the difference between absolute zero and zero degrees Fahrenheit, expressed in degrees with the same size as a Fahrenheit degree; this is called the Rankine scale).

T = T' + 459.7

Now you can compute the scale factor:

(nR/V) = P/T

I inflated my C4's tires to Porsche's standard recommendations for the street (225/40-18 -- 36 PSI at 68 degrees F, 265/35-18 -- 44 PSI at 68 degrees F). Then I took several measurements with my SmarTire system, and averaged them to reduce measurement error. The results were

(nR/V) = 0.0962 [for 225/40-18] (nR/V) = 0.1110 [for 265/35-18]

If you convert this information into equations using ordinary gauge pressure and Fahrenheit temperature, you get these:

P' = 0.0962 * (T' + 459.7) - 14.7 [225/40-18] P' = 0.1110 * (T' + 459.7) - 14.7 [265/35-18]

These are good approximations of the temperature and pressure for the given tire/rim combinations when the initial inflation follows Porsche's recommendations for the street.

Now, suppose you're getting ready for a track session, and want to drop the initial tire pressure. How do the equations change?

Essentially what we want to do is change the value of n in the Ideal Gas Law equation. Fortunately, if the temperature is held constant the equations are linear with respect to n, so we can get a good approximation of the effect of changing it by taking just one more measurement.

I set up this measurement just like the one above, but then I bled enough air from the tires to drop the pressure to about 4 PSI less than Porsche's standard values. The results were

(nR/V) = 0.0886 [225/40-18] (nR/V) = 0.1040 [265/35-18]

So at roughly 4 PSI below stock (measured at 68 degrees F), the equations are

P' = 0.0886 * (T' + 459.7) - 14.7 [225/40-18] P' = 0.1040 * (T' + 459.7) - 14.7 [265/35-18]

Furthermore, from this we can see that changing the initial pressure by 1 PSI changes nR/V by about

0.002 per 1 PSI at 68 degrees F [225/40-18] 0.00175 per 1 PSI at 68 degrees F [265/35-18]

(Keep in mind that these are approximations, and probably have a bit more error than the other variables we've been measuring.)

Now we have what we need in order to make a chart showing how pressure and temperature vary.

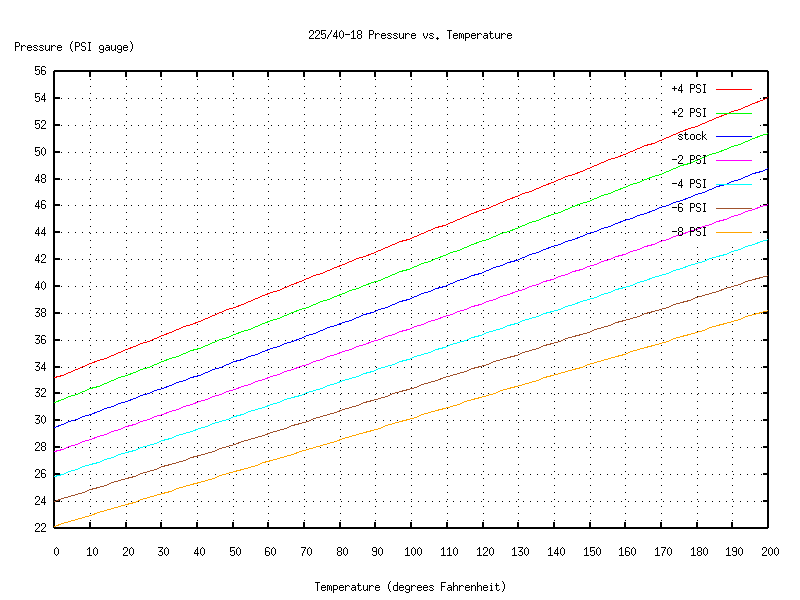
For the fronts:

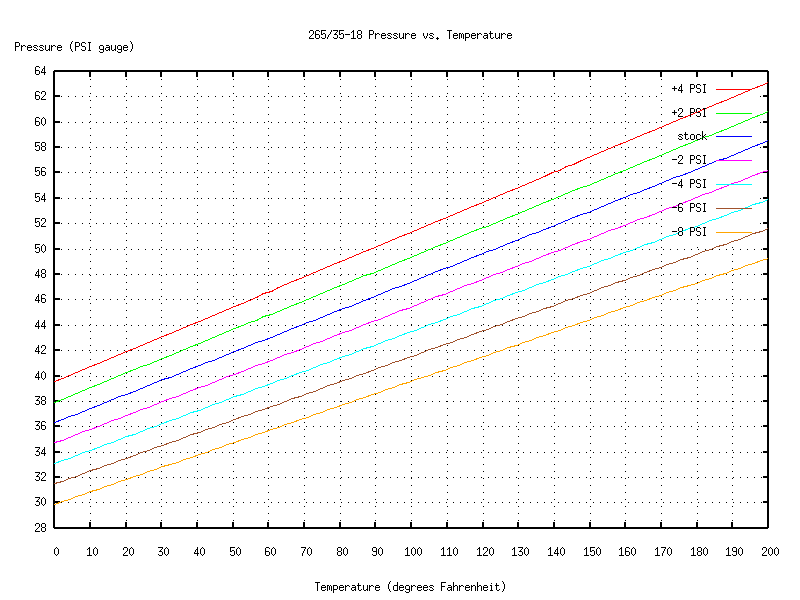
And for the rears:

You can create charts like these for your own tire/rim combinations. But once you have them, how do you use them?

You start by making a measurement of temperature and pressure (waiting for the tires to cold-soak, etc., just like above). Then look on the chart for the line that's closest to your measurement. That line will tell you how the tire's pressure will vary as the internal temperature changes.

What if you don't have charts that describe the behavior of your particular tires and rims? Well, a good rule of thumb is that pressure varies 1 PSI for a temperature change of 10 degrees Fahrenheit. (You can see from the charts or equations that for my tires and rims, that's accurate to about 10%.) So for example, if you measure your tire pressure at 90 degrees Fahrenheit, the "standard" pressure at 68 degrees would be about 2 PSI less than what you measured. If you want, say, 44 PSI at 68 degrees, but it's 90 degrees outside, then put some extra air in your tires, wait for it to adjust to the outside temperature, and bleed or top off the tire until the gauge reads about 46 PSI.

That's it! I hope you found this helpful.